Implicit Differentiation Introduction Consider the function y that is in terms of 2 variables, x and z y 2x 3 4z 2 where z x2 1 If you want to find dx dy (the derivative of y with respect to x), you would naturally replace the z with x2 1 so that you get y 2x 3 4( 1 x2 )2 Now using the chain rule we can find 6x 2 8(dx dy x2 1)( 2x )For example, if y 3 x = 8, y 3x = 8, y 3 x = 8, we can directly take the derivative of each term with respect to x x x to obtain d y d x 3 = 0, \frac{dy}{dx} 3 = 0, d x d y 3 = 0, so d y d x = − 3 \frac{dy}{dx} = 3 d x d y = − 3 Implicit differentiation is especially useful where it is difficult to isolate one of theThe following problems require the use of implicit differentiation Implicit differentiation is nothing more than a special case of the wellknown chain rule for derivatives Find y' = dy/dx for y = x 2 y 3 x 3 y 2 Click HERE to see a detailed solution to problem 4 PROBLEM 5 Assume that y is a function of x

Solutions To Implicit Differentiation Problems
(x+y)^3=x^3+y^3 implicit differentiation
(x+y)^3=x^3+y^3 implicit differentiation-A look at how you can use implicit differentiation (where y isn't the subject) to find a dy/dx derivative using the chain rule, power rule and the product ruFeb 08, 18 · Find \(y'\) by solving the equation for y and differentiating directly Find \(y'\) by implicit differentiation Check that the derivatives in (a) and (b) are the same



How To Derive X 3 Y 3 X Y X 2 Xy Y 2 Quora
IMPLICIT DIFFERENTIATION The equation y = x 2 1 explicitly defines y as a function of x, and we show this by writing y = f (x) = x 2 1 If we write the equation y = x 2 1 in the form y x 2 1 = 0, then we say that y is implicitly a function of x In this case we can find out what that function is explicitly simply by solving for yWe are given the following expression and asked to evaluate the second derivative {eq}\frac{\text{d}^2y}{\text{d}x^2} {/eq} $$5x^34y^3=1 $$ Using implicit differentiationAnswer to Find dy/dx by implicit differentiationx sin y y sin x = 1 Consider the equation To find by implicit differentiation, differentiate both sides of the equation with respect to x Differentiate each term with respect to xAs y is a function of x, differentiate the terms and using Product Rule and Chain Rule
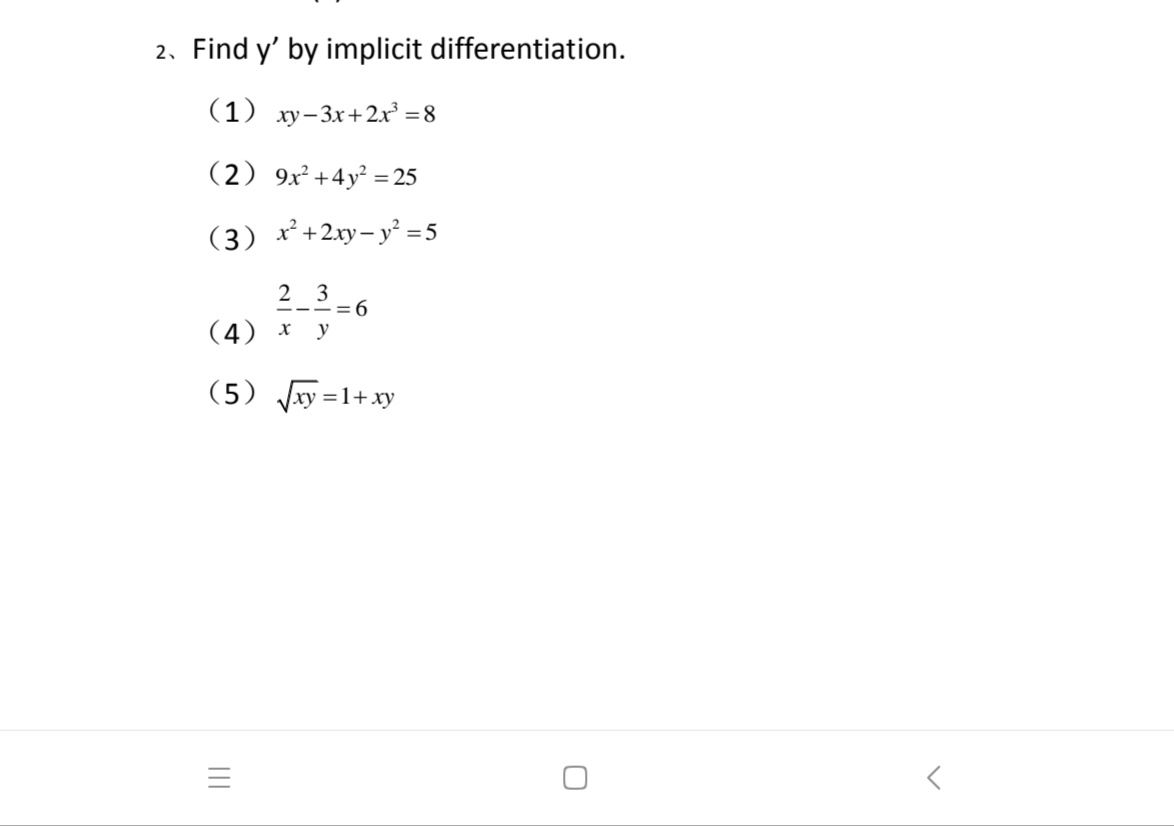
Jun 04, · Y = \\sqrt{(16 x ^{2}}\ and y = \\sqrt{(16 x ^{2}}\ We perform implicit differentiation in such cases The implicit differentiation meaning isn't exactly different from normal differentiation Since we cannot reduce implicit functions explicitly in terms of independent variables, we will modify the chain rule to performCh 26 Find y by implicit differentiation x24y2=4 Ch 26 Find y by implicit differentiation x2xyy2=3 Ch 26 Find y by implicit differentiation sinycosx=1 Ch 26 Find y by implicit differentiation x3y3=7 Ch 26 If xyy3=1, find the value of y at the point whereIMPLICIT DIFFERENTIATION Example 2
For example, the equation latexyx^2=1/latex defines the function latexy=x^21/latex implicitly Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test) We are using the idea that portions of latexy/latex are functions that satisfy the given equation1 Find the derivative using implicit differentiation 2 If both the x and y coordinates are not known find the missing coordinate 3 Substitute the x and y coordinates into the derivative to find the slope of the tangent line 4 Find the equation of the tangent line using the pointslope formula Gerald Manahan SLAC, San Antonio College, 08 4Apr 22, · If you haven't already read about implicit differentiation, you can read more about it here Once you check that out, we'll get into a few more examples below Solution \(\mathbf{3 \ \ x^24xyy^2=4} \) Solution \(\mathbf{4 \ \ \sqrt{xy}=x^4y^4} \) Solution \(\mathbf{5 \ \ e^{x^2y}=xy} \) Solution For each of the above



Math 113 Hw 7 Solutions 3 5
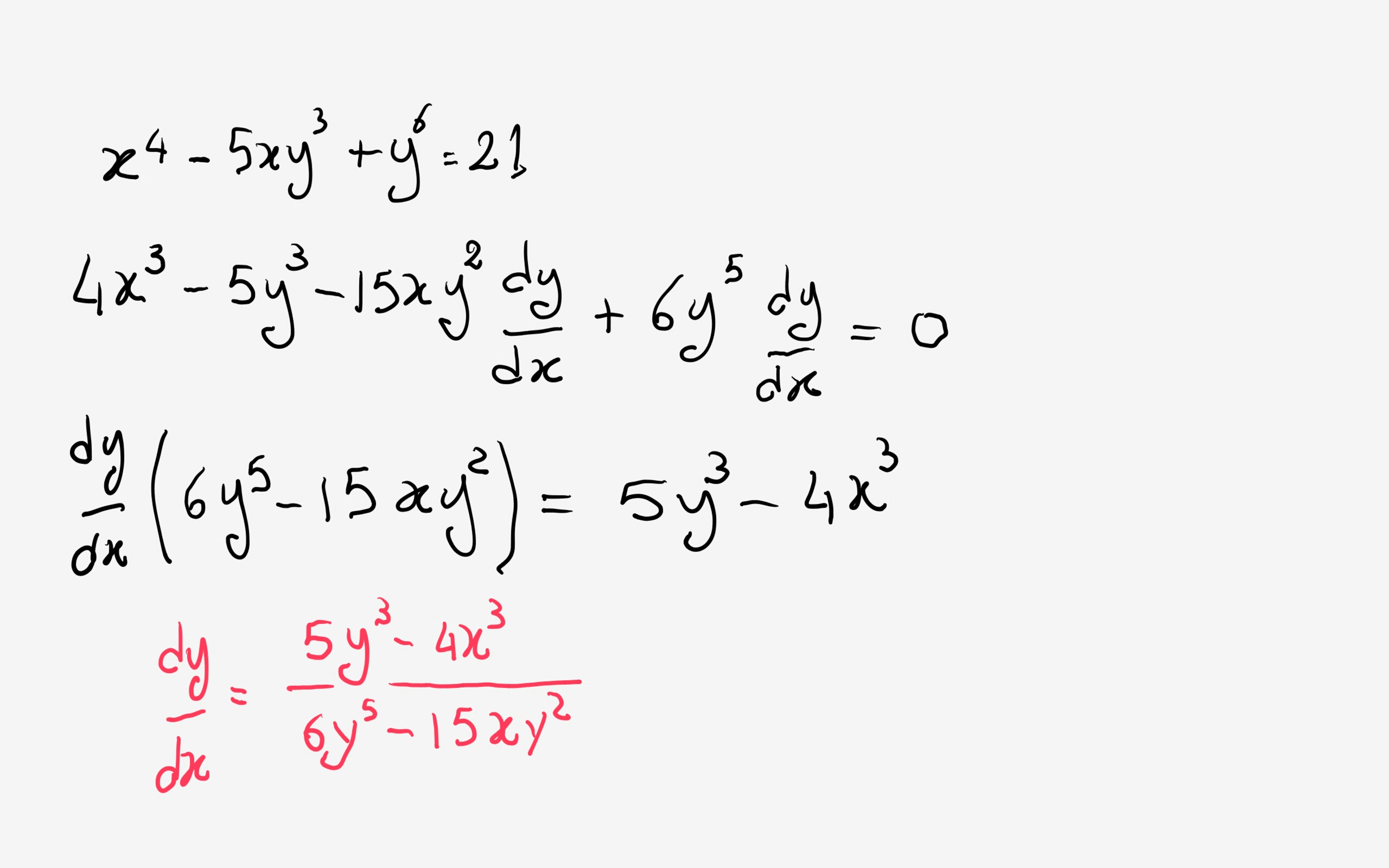


How Do You Find The Implicit Differentiation Of X 4 5xy 3 Y 6 21 Socratic
Learn how to solve implicit differentiation problems step by step online Find the implicit derivative (d/dx)(x^3x*yy^2=7) Apply implicit differentiation by taking the derivative of both sides of the equation with respect to the differentiation variable The derivative of the constant function (7) is equal to zero The derivative of a sum of two functions is the sum of theOct 23, 07 · Re Implicit differentiation jwpaine said For the curve defined by the equation \Lx3 y3 = 3xy \L x 3 y 3 = 3 x y, find an equation of the tangent at the point \L(4 3, 2 3) \L ( 4 3, 2 3) I do \LD(x3 y3) = D(3xy) \L D ( x 3 y 3) = D ( 3 x y) \L3x2 3y2 ⋅y ′Apr 08, 19 · Given is the function $F(x,y,z)=x^2y^3z$ Determine the Jacobian matrix $Dz$ in $P=(1,1,2)$ using implicit differentiation My idea is to calculate $\\frac{∂z


Implicit Differentiation
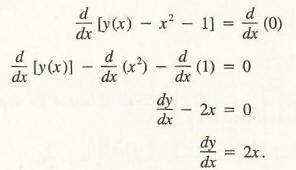


Find A Derivative With Step By Step Math Problem Solver
If a function is described by the equation \(y = f\left( x \right)\) where the variable \(y\) is on the left side, and the right side depends only on the independent variable \(x\), then the function is said to be given explicitlyFor example, the following functions are defined explicitlyBy implicit differentiation x 4 = x y g(x) = t (4x — 3) an h(x) e(X) = (X — sin x Title Image1 Author kpearce Created Date 1//15 PMMay 30, 18 · Section 310 Implicit Differentiation To this point we've done quite a few derivatives, but they have all been derivatives of functions of the form \(y = f\left( x \right)\) Unfortunately, not all the functions that we're going to look at will fall into this form



How To Derive X 3 Y 3 X Y X 2 Xy Y 2 Quora
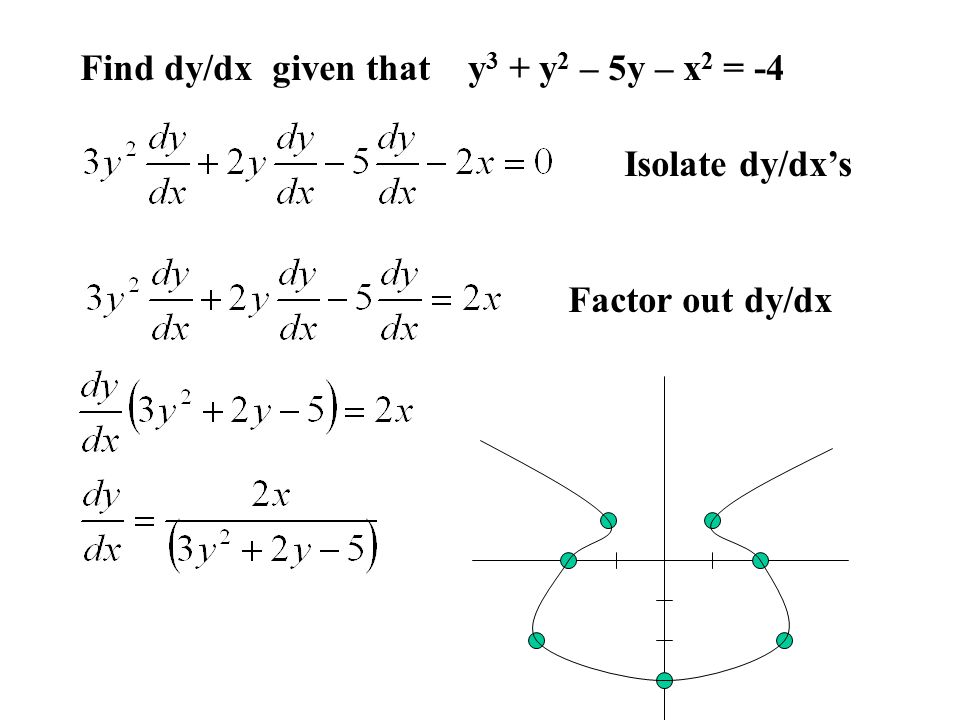


You Can Do It 2 5 Implicit Differentiation How Would You Find The Derivative In The Equation X 2 2y 3 4y 2 Where It Is Very Difficult To Express Ppt Download
Nov 23, 15 · We do this by implicit differentiation The process is to take the derivative of both sides of the given equation with respect to x {\displaystyle x} , and then do some algebra steps to solve for y ′ {\displaystyle y'} (or d y d x {\displaystyle {\dfrac {dy}{dx}}} if you prefer), keeping in mind that y {\displaystyle y} is a function of xImplicit Differentiation As you work through the problems listed below, you should reference Chapter 31 of the recommended textbook (or the equivalent chapter in your alternative textbook/online resource) and your lecture notes The curve below is the graph of \((x^2y^21)^3x^2y^3=0\) Sketch the tangent line to to graph at the pointSep 10, 15 · Now, the given function is (x^3) (y^3) = 1 Differentiating both sides wrt 'x' we get;



Solved Find Dy Dx By Implicit Differentiation X 2 Y 2 Chegg Com
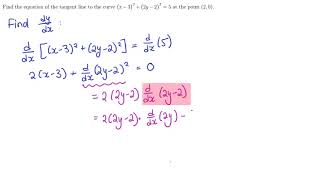


Implicit And Logarithmic Differentiation
Use implicit differentiation to find the largest yvalue in the loop of the Folium of Descartes, which is given by x^3 y^3 3xy = 0 Use implicit differentiation to find the largest yvalue in the loop of the Folium of Descartes, which is given by x 3 y 3 − 3 x y = 0Welcome to Sciemce, where you can ask questions and receive answers from other members of the communityA curve is described by the implicit relationship y xy y x3 = −2 4 10 Find an equation of the normal to the curve at the point where y =1 3 4 15y x = Question 8 A curve has equation 4cos 3 2siny x= − , x∈ , y∈ Show clearly that 4 2y x− = π is the equation of the tangent to the curve at the point with coordinates , 6 3 π π



Ppt 3 7 Implicit Differentiation Powerpoint Presentation Free Download Id



Solved 3 12 Find Dy Dx By Implicit Differentiation B X2 Chegg Com
Your input find $$$\frac{d}{dx}\left(x^{3} y^{3}=2 x y\right)$$$ Differentiate separately both sides of the equation (treat $$$y$$$ as a function of $$$x$$$) $$$\frac{d}{dx}\left(x^{3} y^{3}{\left(x \right)}\right)=\frac{d}{dx}\left(2 x y{\left(x \right)}\right)$$$ Differentiate the lefthand side of the equationThis section covers Implicit Differentiation If y 3 = x, how would you differentiate this with respect to x?Use implicit differentiation to find dy/dx and d2y/dx2xy x y = 3 Find dy/dx by implicit differentiationxy x y x2y2 = 0 asked May 31, 19 in Mathematics by darebornsolja calculus;



Dy Dx X 3y 3 X Y Youtube


Implicit Differentiation
3 Implicit differentiation Example Suppose we want to differentiate the implicit function y2 x3 −y3 6 = 3y with respect x We differentiate each term with respect to x d dx y2 d dx x3 − d dx y3 d dx (6) = d dx (3y) Differentiating functions of x with respect to x is straightforward But when differentiating aCalculus (8th Edition) Edit edition Solutions for Chapter 35 Problem 10E Find dy/dx by implicit differentiationxey = x – y Solutions for problems in chapter 35 1EThere are three ways Method 1 Rewrite it as y = x (1/3) and differentiate as normal (in harder cases, this is not possible!) Method 2 Find dx/dy dx = 3y 2 dy
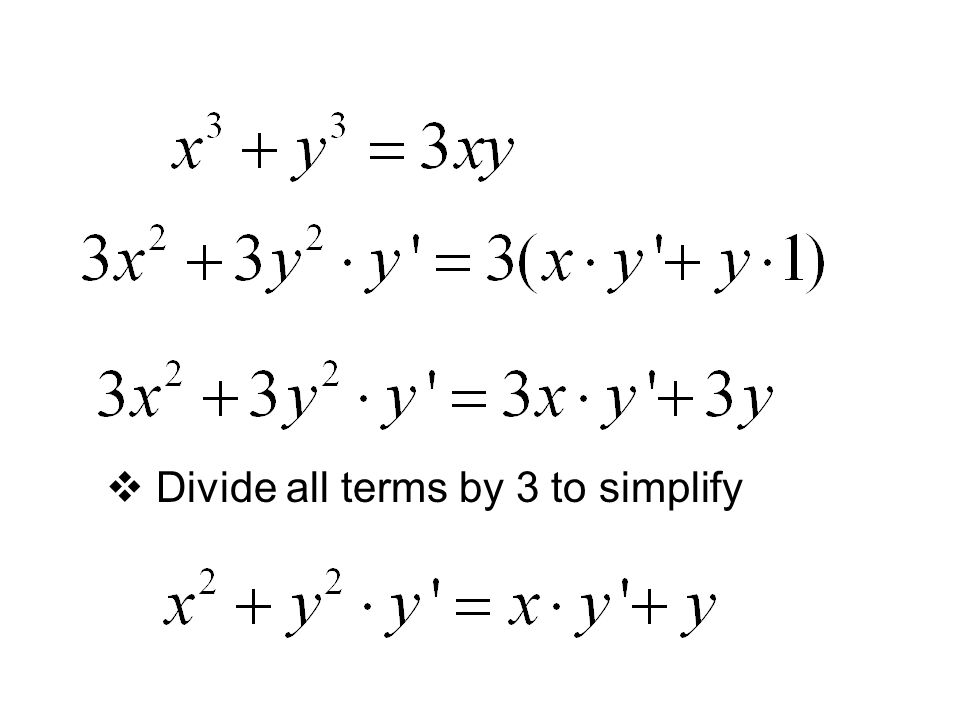


Lesson Derivative Techniques 4 Objective Implicit Differentiation Ppt Download



However Some Functions Are Defined Implicitly Some Examples Of Implicit Functions Are X 2 Y 2 25 X 3 Y 3 6xy Ppt Download
Get an answer for '`x^3 y^3 = 6xy 1, (2,3)` Find `dy/dx` by implicit differentiation and evaluate the derivative at the given point' and find homework helpLet's first write y as an explicit function of x Now, using the product rule, we get Let's try now to use implicit differentiation on our original equality to see if it works out We must use the product rule again in the left side Now we must substitute y as a function of x to compare it to our first result And we got the same result, asImplicit differentiation can help us solve inverse functions The general pattern is Start with the inverse equation in explicit form Example y = sin −1 (x) Rewrite it in noninverse mode Example x = sin(y) Differentiate this function with respect to x on both sides Solve for dy/dx


4 2 Implicit Differentiation



Solved Find Dy Dx By Implicit Differentiation 2x 3 X 2 Chegg Com
Jan 15, 16 · Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange381 Find the derivative of a complicated function by using implicit differentiation 3 Use implicit differentiation to determine the equation of a tangent line We have already studied how to find equations of tangent lines to functions and the rate of change of a function at a specific point In all these cases we had the explicitA Find y' if x3 y3 = 6xy b Find the tangent to the folium of Descartes x3 y3 = 6xy at the point (3, 3) c At what points in the first quadrant is the tangent line horizontal?


4 2 Implicit Differentiation



X 3y 4 X Y 7 Differentiate It And
3 (x^2) 3 (y^2)* (dy/dx) = 0 or, (x^2) (y^2)* (dy/dx) = 0 (1) or, dy/dx = (x^2)/ (yMar 30, 16 · Implicit Differentiation In most discussions of math, if the dependent variable is a function of the independent variable , we express in terms of If this is the case, we say that is an explicit function of For example, when we write the equation , we are defining explicitly in terms of On the other hand, if the relationship between the function and the variable is expressed by anApr 05, 17 · Explanation As (x y)3 = x3 y3, taking differential on both sides implicitly, we get 3(x y)2 ×(1 dy dx) = 3x2 3y2 dy dx or 3 dy dx = 3{x2 − (x y)2} or dy dx = x2 − (x y)2 (x y)2 − y2 or dy dx = − 2xy y2 x2 2xy and at ( − 1,1) dy dx = − 2( −1) × 1 12 12 2( − 1)(1) = − −1 −1 = − 1 Answer link


Answered 2 Find Y By Implicit Differentiation Bartleby
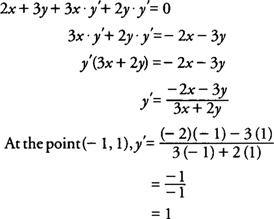


Implicit Differentiation
Answer to Use implicit differentiation to find y' where x^2 6xy 4y^3 = Evaluate this at (x, y) = (2,1) By signing up, you'll getFind dy/dx by implicit differentiation x^3 xy^2 y^3 = 1 Join our free STEM summer bootcamps taught by experts Space is limitedFeb 27, 14 · find dy/dx using implicit differentiation y= 3xy 2x^3 asked Feb 28, 14 in CALCULUS by harvy0496 Apprentice differentiation;



How To Derive X 3 Y 3 X Y X 2 Xy Y 2 Quora



How To Do Implicit Differentiation 7 Steps With Pictures
Jan 31, 13 · Some relationships cannot be represented by an explicit function For example, x²y²=1 Implicit differentiation helps us find dy/dx even for relationships like that This is done using the chain rule, and viewing y as an implicit function of x For example, according to the chain rule, the derivative of y² would be 2y⋅(dy/dx)Use implicit differentiation to find an equation of the tangent line to the ellipse x^2/2 y^2/8 = 1 at (1, 2)May 21, · Thus at the point (3√6, 0), we have the slope as y′ = − 3(3√6)2 cos0 3 ⋅ 02 = − 33√36 1 ≈ − 991 Therefore the equation of the tangent line to the implicitly defined function siny y3 = 6 − x3 at the point (3√6, 0) is y = − 33√36(x − 3√6) 0 ≈ − 991x 18 The curve and this tangent line are shown in Figure 2



Implicit Differentiation



How To Do Implicit Differentiation 7 Steps With Pictures
Find y" by implicit differentiation x^2 xy y^2 = 3 Join our free STEM summer bootcamps taught by experts Space is limited


4 2 Implicit Differentiation



Implicit Differentiation


3 8 Implicit Differentiation Calculus Volume 1



Solved Dy 11 If X Xy 3y 3 Then At The Point 2 Chegg Com
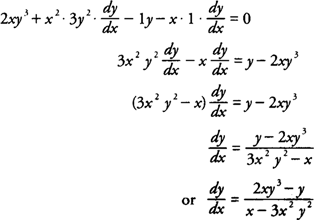


Implicit Differentiation



How To Factorise Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube



If 3x 2y 3 And X 2 Y 2 130 Then What Can Be The Value Of X And Y Quora


Implicit Differentiation
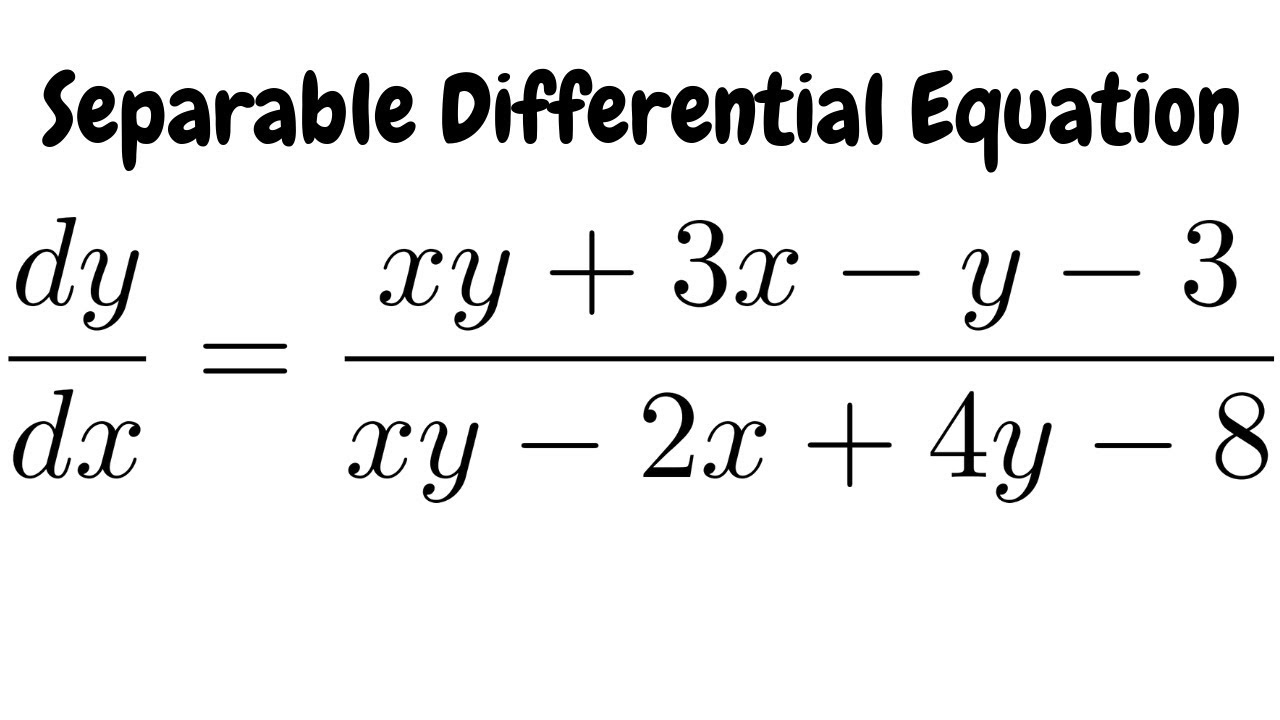


Separable Differential Equation Dy Dx Xy 3x Y 3 Xy 2x 4y 8 Youtube
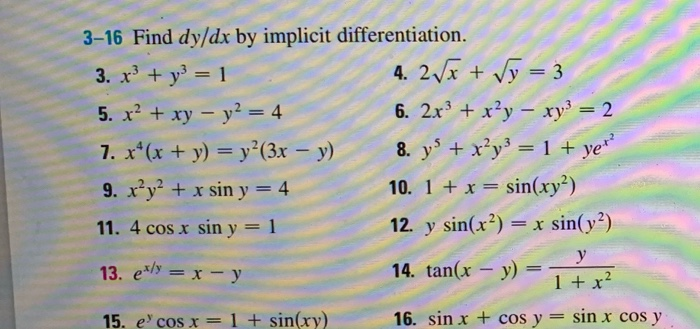


Solved 3 16 Find Dy Dx By Implicit Differentiation 4 2x Chegg Com



Implicit Differentiation However Some Functions Are Defined Implicitly
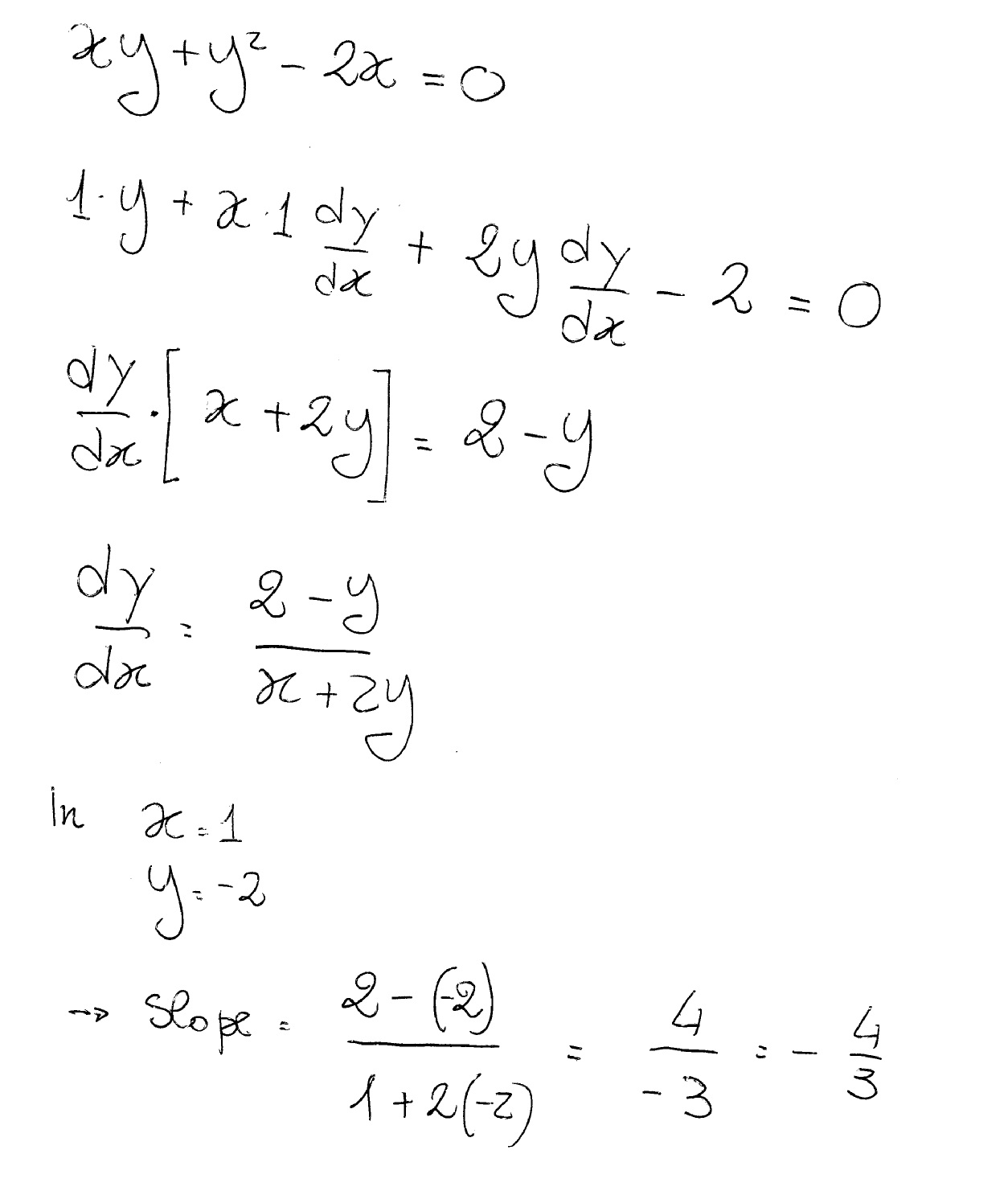


How Do You Differentiate Implicitly Xy Y 2x 0 To Find Dy Dx And Find The Slope Of The Curve At The Given Point 1 2 Socratic


If X 3 Y 3 3axy 0 Then Prove That D 2y Dx 2 2a 2xy Ax Y 2 3 Sarthaks Econnect Largest Online Education Community
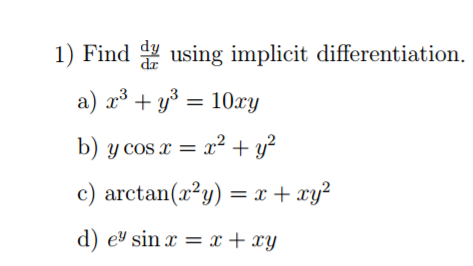


Solved Find Dy Dx Using Implicit Differentiation A X 3 Chegg Com
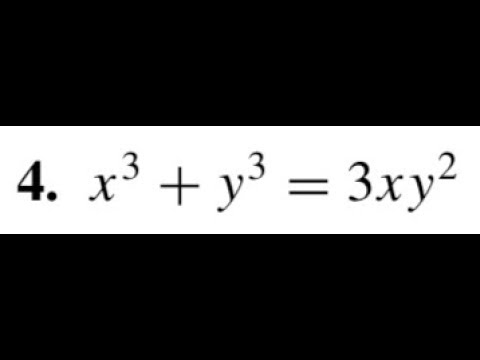


X 3 Y 3 3xy 2 Find Dy Dx Using Implicit Differentiation Youtube
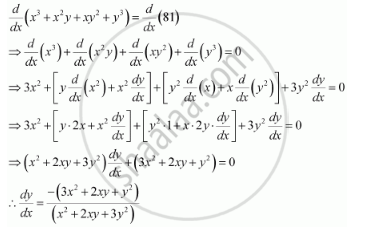


Find Dy Dx For X3 X2y Xy2 Y3 81 Mathematics Shaalaa Com


4 2 Implicit Differentiation


Differentiation



Chapter 04



12 Math 1 Comm Pages 101 150 Flip Pdf Download Fliphtml5



4 1 Implicit Differentiation



Ex 5 3 6 Find Dy Dx In X3 X2y Xy2 Y3 81 Cbse
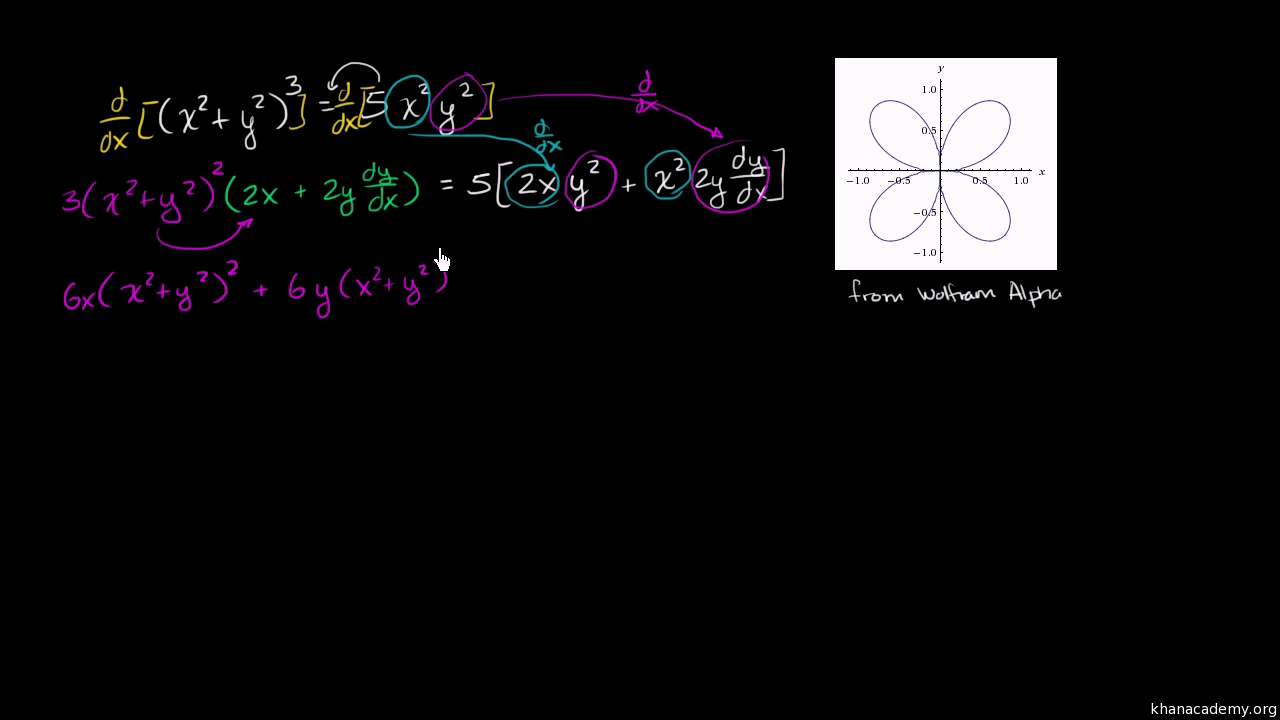


Implicit Differentiation Advanced Example Video Khan Academy



Implicit Differentiation Advanced Example Video Khan Academy


5 Derivative Of The Logarithmic Function
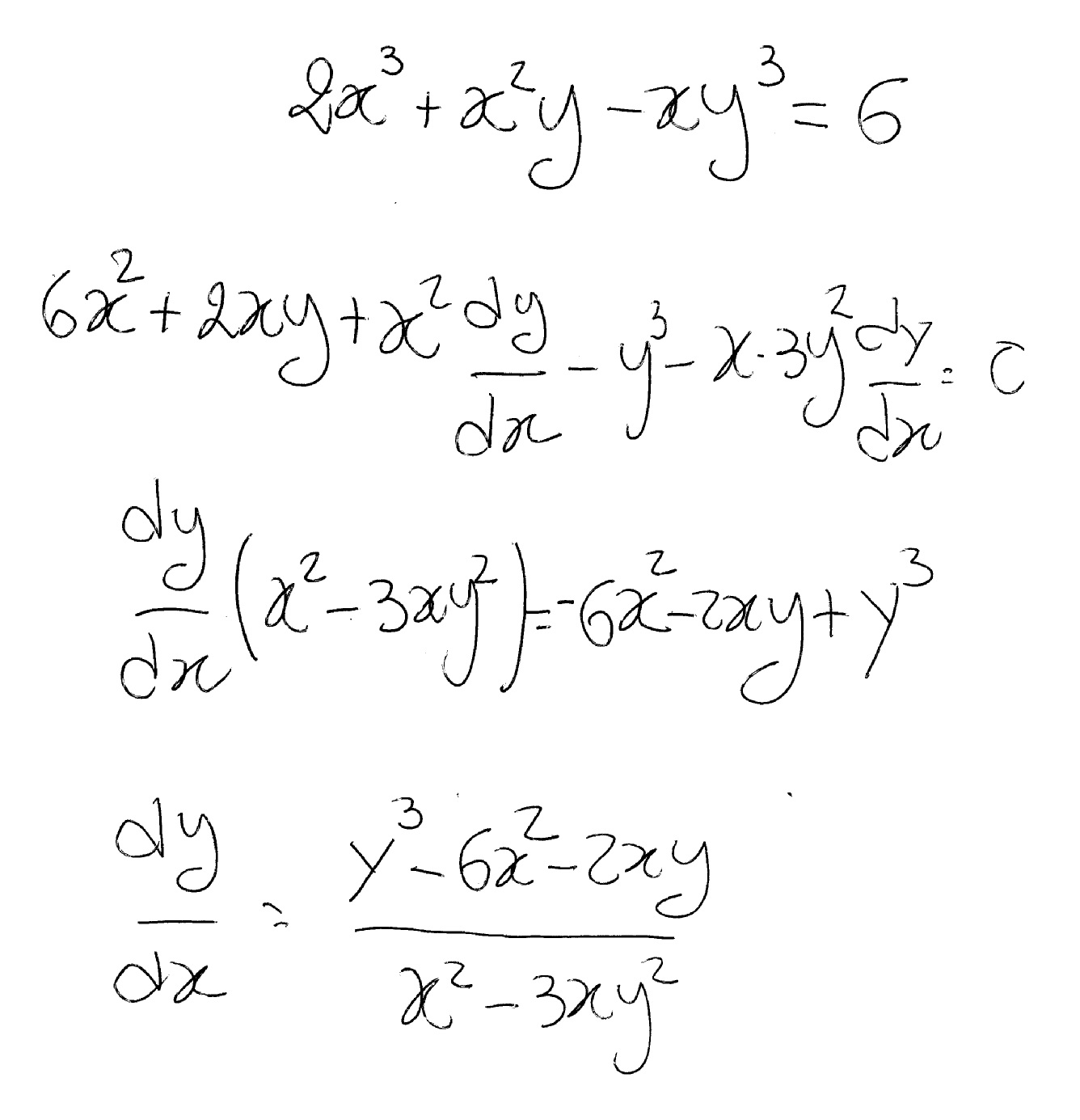


How Do You Find Dy Dx By Implicit Differentiation For 2x 3 X 2 Y Xy 3 6 Socratic



Section 3 6 1 Implicitly Differentiate To Find Dy Dx Y3 X2 4 Slideshow And Powerpoint Viewer 2 Implicitly Differentiate To Find Dy Dx Y 4 X 3 2x 3 Implicitly Differentiate To F



Find The Derivative Of X 3 Xy Y 3 1 Youtube



High School Grade 12 Calculus How To Find Dy Dx For X 3y 6 Number 1 I Just Don T Understand How Implicit Differentiation Works I Know The Answer Because Of The Answer Key
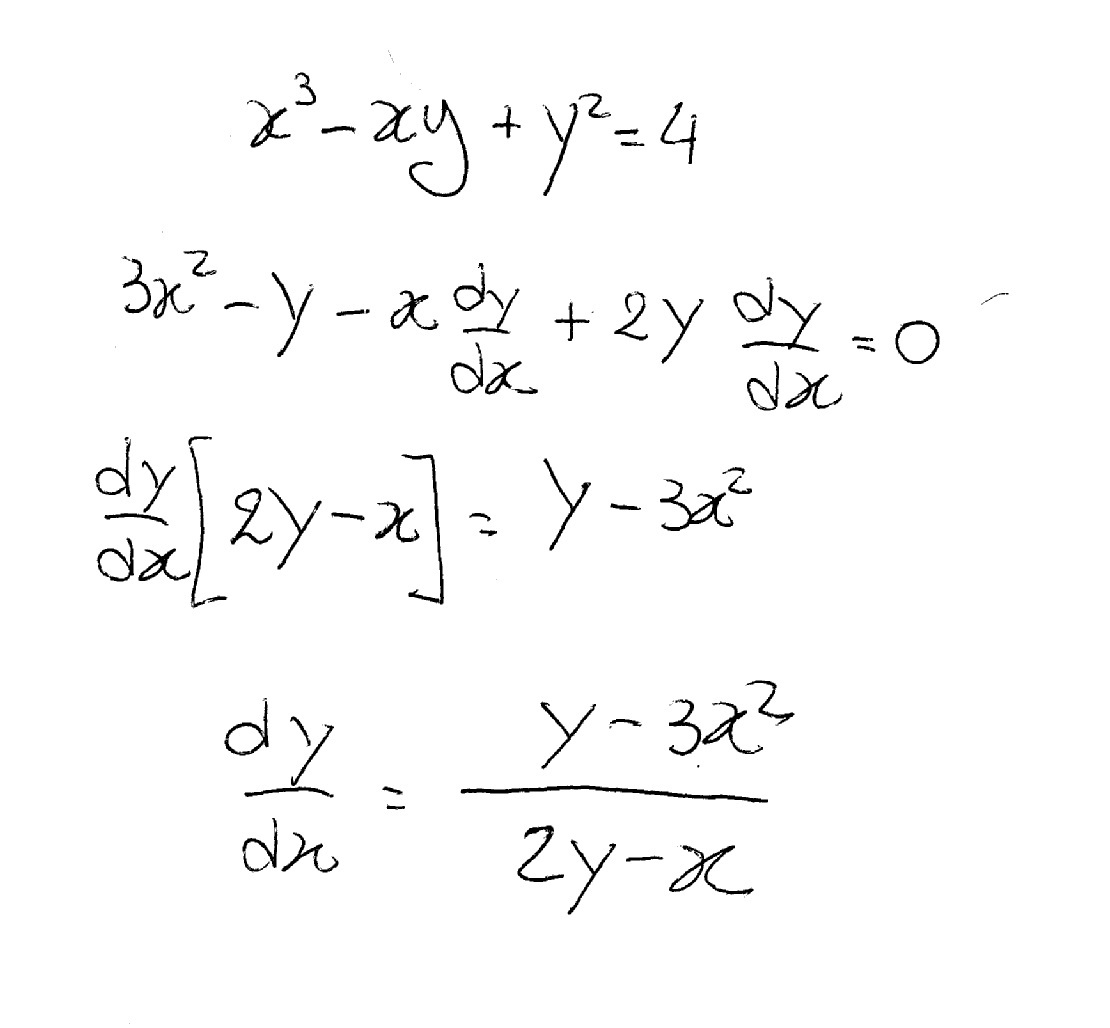


How Do You Differentiate X 3 Xy Y 2 4 Socratic


What Is The Partial Derivative Of X 3y Xy 3 With Respect To X Quora



Answered Us Sec ఇప 2 5 Implicit Differentiation Bartleby
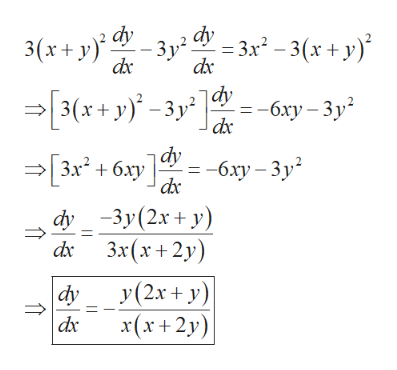


Answered Us Sec ఇప 2 5 Implicit Differentiation Bartleby
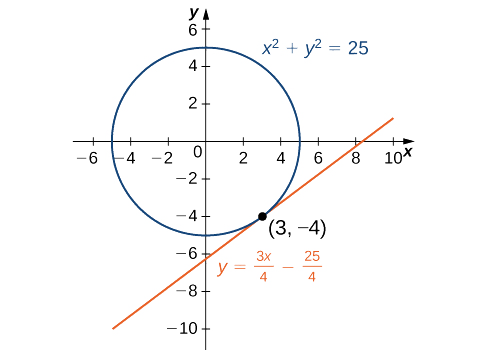


3 8 Implicit Differentiation Mathematics Libretexts



Introduction To Calculus Book Chapter Iopscience



Solutions To Implicit Differentiation Problems



You Can Do It 2 5 Implicit Differentiation How Would You Find The Derivative In The Equation X 2 2y 3 4y 2 Where It Is Very Difficult To Express Ppt Download
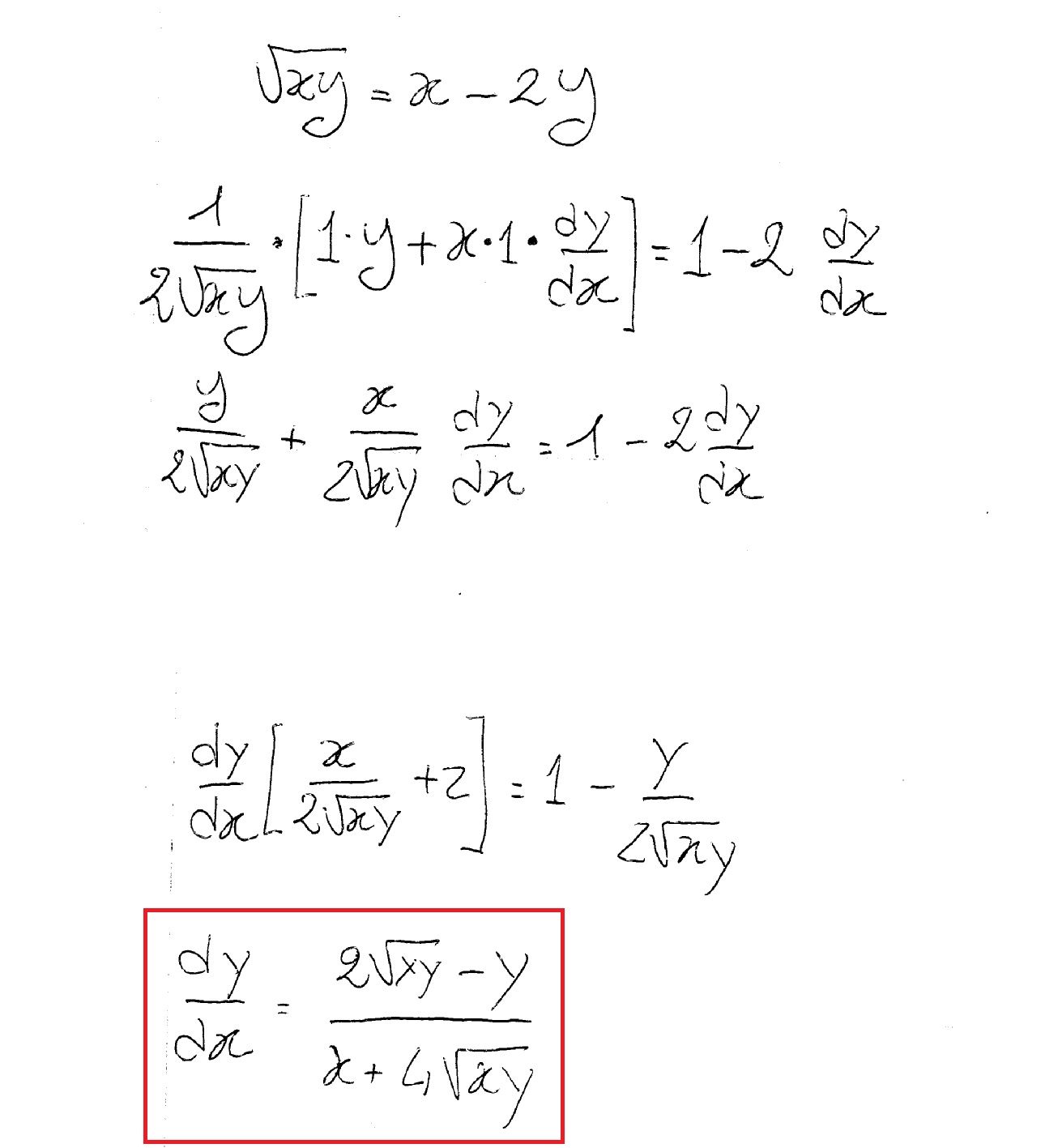


How Do You Differentiate Sqrt Xy X 2y Socratic



Sheet 1 Implicit Diff
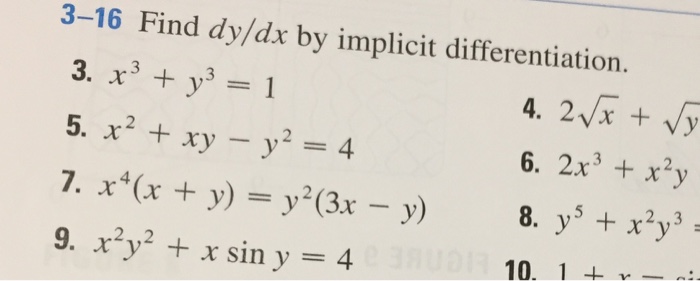


Solved Find Dy Dx By Implicit Differentiation 3 X 3 Y Chegg Com



Implicit Differentiation If 2 X 2 3 X Y Y 2 X 2 Y 8 0 Then Frac 4 Y 2 1 Frac 3 Y 4 X 1 2 Y 3 X 2 2 Frac 3 Y 4 X 1 2 Y 3 X 2 3 Frac 3 Y 4 X 1



X3 Y3 3axy 0 Find Dy Dx Brainly In



C6cocdocnmj3rm



Find The Derivative Of X 3y 3 Y X Using Implicit Differentiation Youtube



Implicit And Logarithmic Differentiation
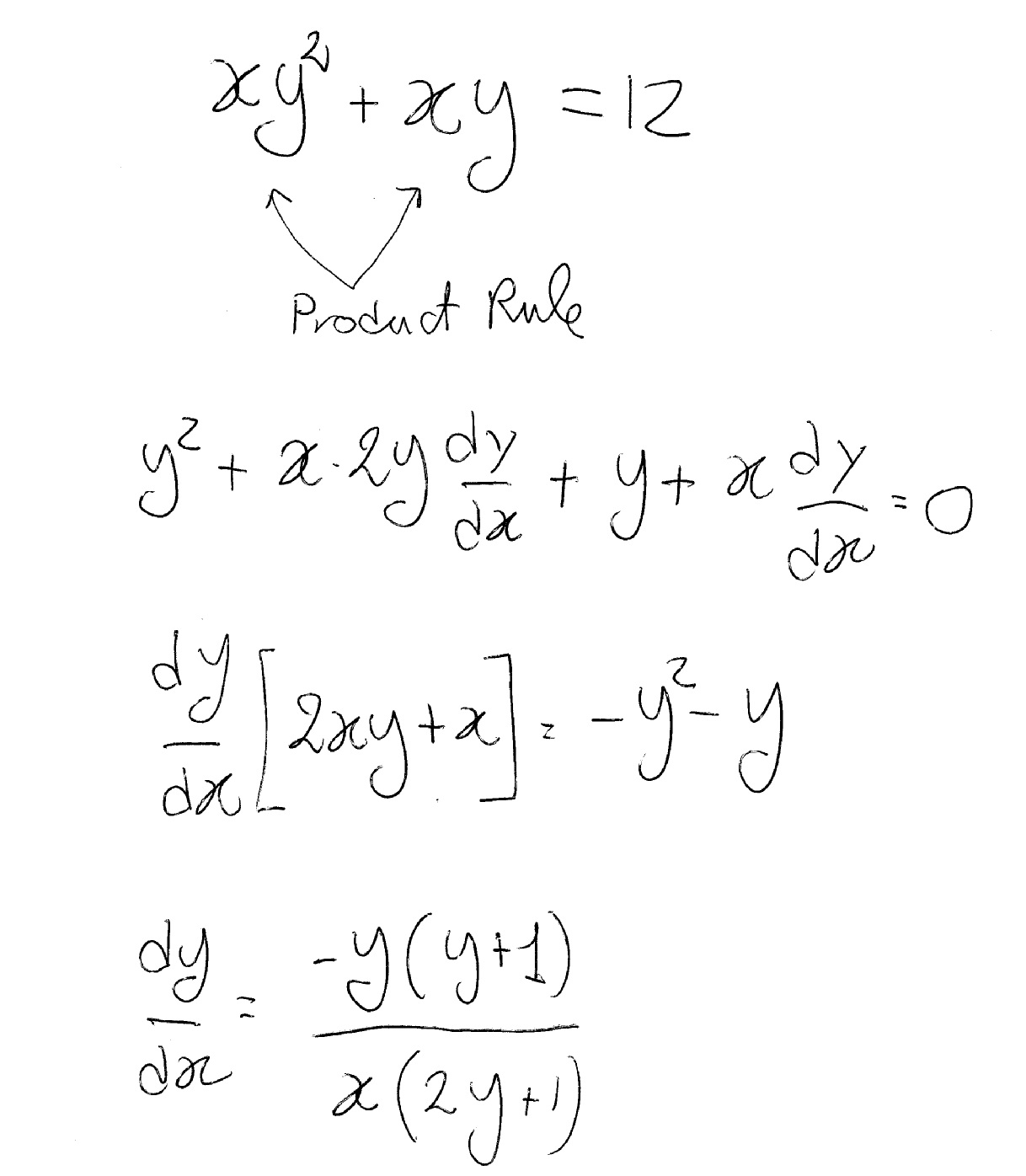


How Do You Differentiate Xy 2 Xy 12 Socratic



If X 2 Y 3 X 3y 2 Then Dy Dx Youtube



Pdf Ism T11 C03 C Pdf Samuel Boroni Academia Edu



Find Dy Dx If X 3 Y 3 3axy Brainly In


3 8 Implicit Differentiation Calculus Volume 1



4 1 Implicit Differentiation


Implicit Differentiation Hsn Forum
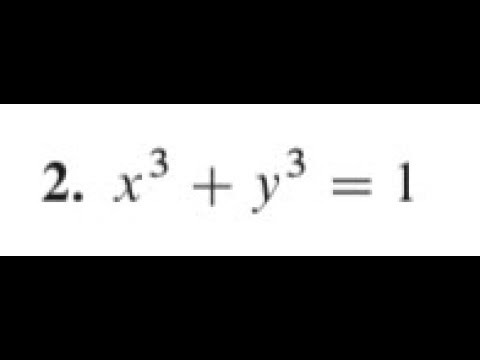


Derivative Of X 3 Y 3 1 Using Implicit Differentiation Youtube



Implicit Differentiation Advanced Example Video Khan Academy



Implicit Differentiation



How To Do Implicit Differentiation 2x 2y Y 3 5 Youtube



If X 3 2x 2y 2 5x Y 5 0 And Y 1 1 Then A Y Prime 1 4


Math Ebook Implicit Differentiation



4 1 Implicit Differentiation


Differentiation



Solved Use Implicit Differentiation To Find Dy Dx In Exer Chegg Com
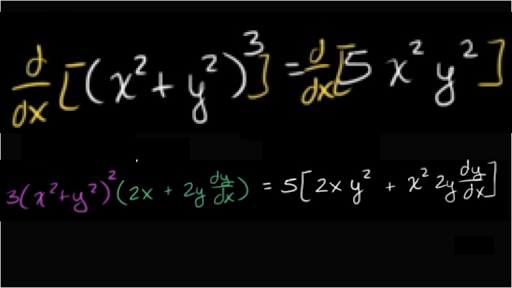


Implicit Differentiation Advanced Example Video Khan Academy


3 7 Implicit Differentiation



4 1 Implicit Differentiation
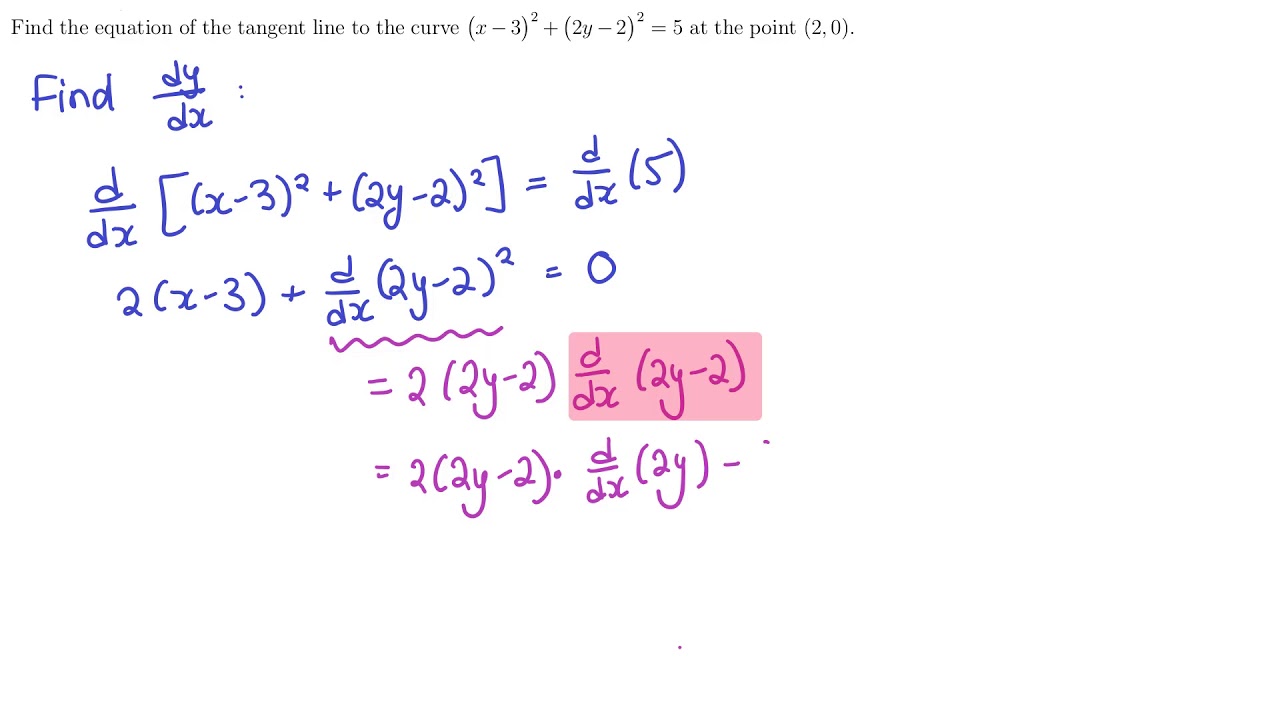


Implicit And Logarithmic Differentiation



Implicit Differentiation However Some Functions Are Defined Implicitly



14 2 Limits And Continuity



In Exercises 1 16 Find Dydi B See How To Solve It At Qanda



For Each Problem Use Implicit See How To Solve It At Qanda



If 3 X 3 Y 3 X Y Then What Is Dy Dx Equal To



Examples Using Implicit Differentiation Solutions Formulas Videos



0 件のコメント:
コメントを投稿